
If we only have two unknowns, it’s easy to map these to a two-dimensional x-y plane.Ĭontinuing with the same two-equation example above, we could convert both equations to slope-intercept form:Įxercise Click the “circuit,” click “Simulate,” then “Run DC Sweep.” You’ll see the two lines plotted, with an intersection at x = 2, y = 1

The variable yĬan’t both increase and decrease at the same time. To increase a little bit to remain valid, and the other equation would require it to decrease. Why? Because if, for example, we were to increase xīy a little bit, then one equation would require y In fact, it is a unique solution point: it is the only solution to this system. All of the equations must be true for the solution to be valid. But it will make the second equation false. , this will make the first equation true. We have to choose specific values for all of the unknowns in order to evaluate the left-hand sides of each equation, so we are searching over all possible values of all unknowns. Let’s search for a solution by trying different values for the unknowns. When we jump to having multiple equations and multiple unknowns, we have to think about not just whether our one equation is a true statement, but whether all of the equations in our system are true at the same time and for the same values of the unknowns.Ĭonsider this system of two linear equations in two unknowns: In this case, this equation is a true statement only when y = 2 It is only a true statement at one particular choice. Is a false statement for infinitely many possible choices of y The equation is true when the left side equals the right side.įor most values of the unknowns, the equation will be false: y + 1 = 3
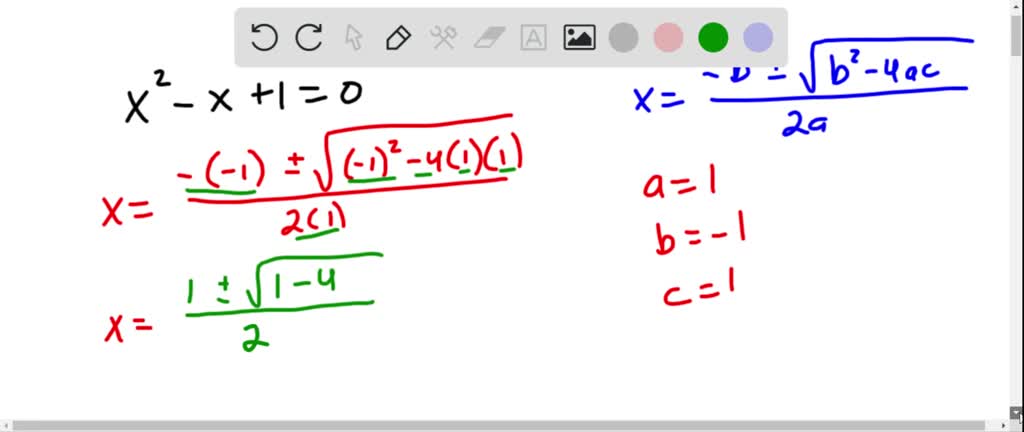
These sorts of equations will not be addressed here, but are still solvable with multiple numerical iterations using the same techniques shown here as a foundation.Ī system of equations simply means that we have multiple equations, all of which must be satisfied at the same time, and multiple unknowns, which are shared between the equations.Īn equation with unknowns is a search problem: we are searching for the value of the unknowns that will make the equation be true.

Empirical results reveal that the proposed approach is able to deal with highdimensional equations systems.Y = sin ( x ) has non-linear function inside x 2 = 1 has polynomial term of order 2 x ( y + 1 ) = 3 has product of unknowns Several well-known and difficult applications (such as interval arithmetic benchmark, kinematic application, neuropsychology application, combustion application, and chemical equilibrium application) are considered for testing the performance of the new approach. The results obtained are compared with a very new technique that is considered as efficient and is also compared with some of the standard techniques that are used for solving nonlinear equations systems. An evolutionary computation technique is applied to solve the problem obtained by transforming the system into a multiobjective optimization problem. Every equation in the system represents an objective function whose goal is to minimize the difference between the right and left terms of the corresponding equation. This paper proposes a new perspective for solving systems of complex nonlinear equations by simply viewing them as a multiobjective optimization problem.


 0 kommentar(er)
0 kommentar(er)
